MENU
  1. ホーム
  2. テクノロジー
  3. AI（人工知能）
  4. 【機械学習入門】これならわかる！オートエンコーダーの使い方！

【機械学習入門】これならわかる！オートエンコーダーの使い方！

AI（人工知能）
フクロウ

データの次元圧縮や、ディープラーニングのプレトレーニングにも使われるオートエンコーダについて、この記事では紹介していきます。

オートエンコーダの簡単な実装方法、学習させたモデルがどういう使い方をできるのかについてチェックして行きましょう。

この記事でわかること

  • オートエンコーダとは？
  • オートエンコーダのPython実装
  • 更に詳しく学ぶ方法

名前は聞いたことがあるけど試したことはない、そんな方はこの記事で一緒にオートエンコーダについて学んでいきましょう！

目次

オートエンコーダとは

オートエンコーダとは、ニューラルネットワークの構造を使った次元圧縮手法です。

ニューラルネットワークには出力層から出てくる出力値がありますが、このオートエンコーダではどちらかというと中間層のニューロンの値の方が大切です。

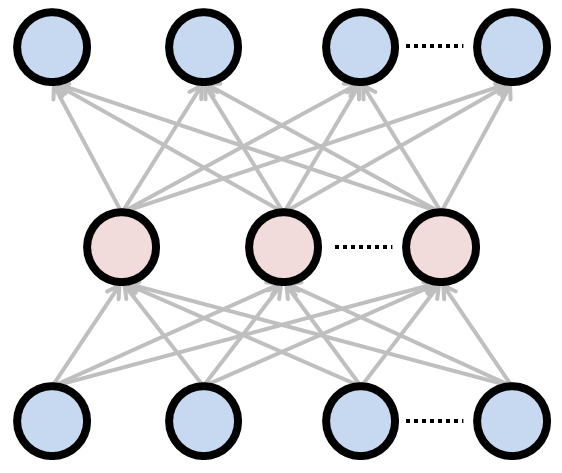
[オートエンコーダのイメージ（下から、入力層、中間層、出力層）: http://nkdkccmbr.hateblo.jp/entry/2016/10/06/222245 より]

最も一般的なオートエンコーダは、中間層に「入力データを圧縮したい次元数」のニューロンを用意します。

一般的には入力次元よりも小さめに。

そして出力層では入力データを再現するような出力値を出します。

一度小さい次元にデータを埋め込んで（エンコードして）、エンコードしたデータを元に、入力データを再び再構築します。

つまり、エンコードされたデータは、本来より小さい次元数でデータを表現できていると言えます。

この中間層のデータを使って可視化を行ってもいいですし、他のアルゴリズムの入力データとして使ってもいいですね。

オートエンコーダの実装

実際にオートエンコーダを実装してみましょう。

以降の実装は

を参考にして修正を加えたものを使っています。

また、Jupyter labでのハンズオンを想定しています。

ライブラリのimport

import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt

実装で楽をするために、tensorflowのkeras apiを使います。

生のtesnorflowを使うよりも簡単にニューラルネットワークが実装できるのでおすすめです。

データの読み込み

(train_images, train_labels), (test_images, test_labels) = keras.datasets.mnist.load_data()

kerasのdatasetsモジュールからmnistをダウンロードして使います。

このデータセットは28×28ピクセルの手書きの数字画像が集められたデータセットです。

# データセットのサイズをチェック
train_images.shape

# (60000, 28, 28)

test_images.shape

# (10000, 28, 28)

train_images = train_images / 255.0

test_images = test_images / 255.0

ではデータセットの中身を見てみましょう。

plt.figure(figsize=(10,10))
for i in range(25):
    plt.subplot(5,5,i+1)
    plt.xticks([])
    plt.yticks([])
    plt.grid('off')
    plt.imshow(train_images[i], cmap=plt.cm.binary)
    plt.xlabel(train_labels[i])

MNISTは比較的簡単な画像分類タスクなので、オートエンコーダの動きを確かめるにはちょうどいい感じです。

モデルの定義

ではtensorflow.kerasを使ってモデルを定義します。

model = keras.Sequential([
    keras.layers.Dense(32, activation=tf.nn.relu),
    keras.layers.Dense(28*28, activation=tf.nn.sigmoid)
])

keras.Sequentialの中に、ニューラルネットワークのレイヤーを追加していくだけでOKです。

activationに渡しているのが活性化関数なので、適切なものを選びましょう。

model.compile(optimizer=tf.train.AdamOptimizer(), 
              loss='binary_crossentropy',
              metrics=['mean_squared_error','binary_crossentropy'])

モデルを組んだらコンパイルを行います。

この処理をしないとtesnorflowでの計算ができないので注意してください。

optimizerはbackpropagationを効率的に行うためのアルゴリズムを指定できます。

lossは学習中に最小化する損失関数です。

metricsは学習のモニタリングを行う際に人間が見るものなので、学習とは関係がありません。

モデルの学習

学習はsklearnと同様に、fitメソッドで行なえます。

x_train = train_images.reshape((len(train_images), np.prod(train_images.shape[1:])))
x_test = test_images.reshape((len(test_images), np.prod(test_images.shape[1:])))

model.fit(x_train, x_train, epochs=20, batch_size=256)

epochsは学習ループの回数、batch_sizeには一度に学習するデータのサイズを指定します。

batch_sizeは学習に使うコンピュータのスペックなどに合わせて決めてください。

[学習中のログ]

Epoch 1/20
60000/60000 [==============================] - 1s 17us/step - loss: 0.0941 - mean_squared_error: 0.0103 - binary_crossentropy: 0.0941
Epoch 2/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0939 - mean_squared_error: 0.0103 - binary_crossentropy: 0.0939
Epoch 3/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0938 - mean_squared_error: 0.0103 - binary_crossentropy: 0.0938
Epoch 4/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0937 - mean_squared_error: 0.0102 - binary_crossentropy: 0.0937
Epoch 5/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0936 - mean_squared_error: 0.0102 - binary_crossentropy: 0.0936
Epoch 6/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0935 - mean_squared_error: 0.0102 - binary_crossentropy: 0.0935
Epoch 7/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0935 - mean_squared_error: 0.0102 - binary_crossentropy: 0.0935
Epoch 8/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0934 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0934
Epoch 9/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0933 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0933
Epoch 10/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0933 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0933
Epoch 11/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0933 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0933
Epoch 12/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0932 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0932
Epoch 13/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0932 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0932
Epoch 14/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0931 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0931
Epoch 15/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0931 - mean_squared_error: 0.0101 - binary_crossentropy: 0.0931
Epoch 16/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0931 - mean_squared_error: 0.0100 - binary_crossentropy: 0.0931
Epoch 17/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0930 - mean_squared_error: 0.0100 - binary_crossentropy: 0.0930
Epoch 18/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0930 - mean_squared_error: 0.0100 - binary_crossentropy: 0.0930
Epoch 19/20
60000/60000 [==============================] - 1s 11us/step - loss: 0.0930 - mean_squared_error: 0.0100 - binary_crossentropy: 0.0930
Epoch 20/20
60000/60000 [==============================] - 1s 12us/step - loss: 0.0930 - mean_squared_error: 0.0100 - binary_crossentropy: 0.0930
<tensorflow.python.keras.callbacks.History at 0x7f84567cc5c0>

学習中もこのように進捗具合が確認できます。

ここのログを出す機能を自分で作らなくてもいいのがkerasのいいところですね。

再構成された画像の確認

それでは、中間層を32次元にして圧縮しているオートエンコーダが、実際にどのような画像を再構成しているのかをチェックします。

きれいに再構成できていれば良い特徴が取れていることが期待できます。

x_recon = model.predict(x_test)

n_images = 10
plt.figure(figsize=(20, 4))
for i in range(n_images):
    # テストデータのオリジナルを表示
    ax = plt.subplot(2, n_images, i+1)
    plt.imshow(x_test[i].reshape(28, 28), cmap=plt.cm.binary)
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.xlabel(class_names[train_labels[i]])

    # テストデータのデコードしたものを表示
    ax = plt.subplot(2, n_images, i+1+n_images)
    plt.imshow(x_recon[i].reshape(28, 28), cmap=plt.cm.binary)
    ax.get_xaxis().set_visible(False)
    ax.get_yaxis().set_visible(False)
    plt.xlabel(class_names[train_labels[i]])

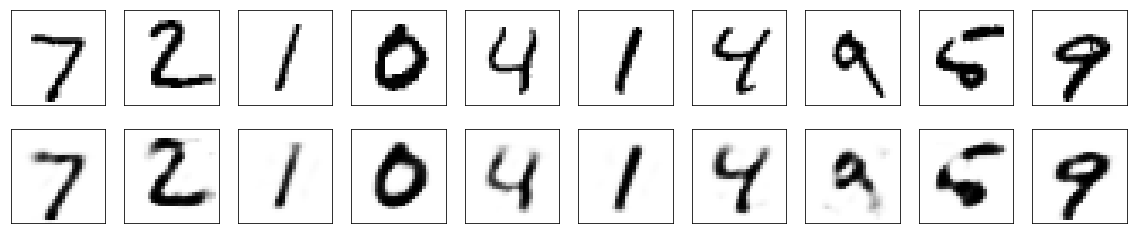
特にチューニングしなくても、結構きれいに再構成できていることがわかりました。

後は中間層のニューロンの値を活用するだけですね！

もっと深く学ぶには

オートエンコーダやその他のDeep Learningについて学びたいならば、書籍やオンライスクールがおすすめです。

Deep LearningはPythonライブラリのおかげで比較的簡単に実装できるようになりました。

ですが必要となる前提知識が多すぎてなかなか独学では勉強が難しいです。

もっと基礎から、例えば「Pythonってどうやってインストールすればいいの？」から「ビジネスの現場で役立つデータ解析方法を最短で学びたい」と思ったならば、侍エンジニアのマンツーマンレッスンがおすすめです。

[su_button url=”https://lp.sejuku.net/lp1_blog_01/?cid=ai_btn1_63331″ target=”blank” background=”#ffffff” color=”#ff9a8f” size=”9″ center=”yes” radius=”10″ icon=”icon: external-link” icon_color=”#fff88f” text_shadow=”0px 0px 10px #808080″]侍エンジニアとは？
詳細はこちらから[/su_button]

仕事に役立つようなデータ解析手法の習得を3ヶ月や6ヶ月の期間、インストラクターとマンツーマンで勉強できます。

是非考えてみて下さい！

まとめ

この記事ではオートエンコーダについて紹介しました。

オートエンコーダはDeep Learningが最初に流行った頃から使われている古典的なモデルです。

ですがこれを元にしたモデルがたくさんありますし、なんと言っても様々な応用が効く点から見ても面白いので、是非勉強してみてくださいね！

AI（人工知能）
AI python

この記事を書いた人

フクロウのアバター フクロウ

第一言語はPythonです。
皆さんRustやりましょう。

この著者の記事一覧へ
目次