ニューラルネットワーク、深層学習を体系的に勉強していくにあたって、いろいろな解説書で最初に解説されるアルゴリズムが「単純パーセプトロン」です。
ニューラルネットワークを勉強していくにあたって、まず最初に知ってほしいアルゴリズムだと言えます。
単純パーセプトロンの仕組みを知って、「このアルゴリズムが何ができて何ができないのか」を理解しましょう。
この記事で解説すること
- 単純パーセプトロンとは
- 単純パーセプトロンでできること
- 単純パーセプトロンでできないこと
単純パーセプトロンとは
「パーセプトロン」とは、複数の入力データ(入力信号)に対して、一つの値を出力する関数です。
後述しますが、パーセプトロンを複数組み合わせるアルゴリズムもありますので、一つしか使わないものを単純パーセプトロンと呼びます。
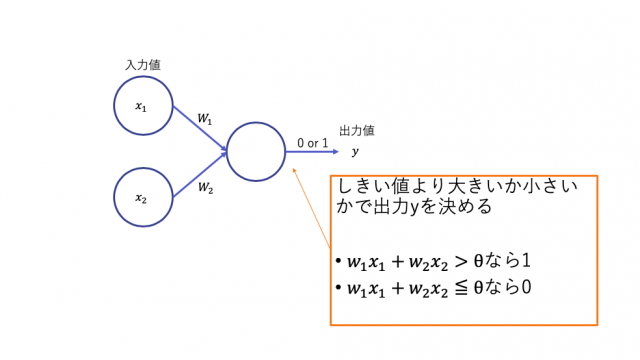
入力信号をx1, x2で表します。
また、出力信号をyとしました。
ここで、各入力信号とは、あるデータの特徴を表します。
それぞれの特徴が目的の値(y)を計算するときにどの程度重要なのかを表すパラメータ(結合重み)として、w1,w2を使います。
図中の数式のように入力信号と、それに対応するwをかけあわせた値をすべて足し合わせた値を出しましょう。
この値がしきい値θ以下ならば0、しきい値θより大きければ1を返す関数がパーセプトロンです。
このパーセプトロンを使うと、簡単な分類問題などを解くことができます。
単純パーセプトロンの例題
ANDゲートを用意する
単純パーセプトロンの例題として、よく論理演算をパーセプトロンで実装するものがあります。
ここでも、単純パーセプトロンを使って、ANDゲートを実装してみましょう。
まずはライブラリのimport。
import pandas as pd import numpy as np import matplotlib import matplotlib.pyplot as plt
ANDゲートの表を作ってみます。
signal = pd.DataFrame(
[
[0,0],
[1,0],
[0,1],
[1,1]
],
columns = ["x1", "x2"]
)
この記事ではANDゲートについてのみ解説しますが、実際に手元で勉強していく際には、ORゲートなどのものも試してみてください。
signal変数に論理値の入力信号をまとめました。
これを元にして他の論理演算も試してみてくださいね。
さて、ANDゲートの正解データをDataFrameで作ってみましょう。
# AND AND = signal.copy() AND["y"] = signal.x1 & signal.x2 AND
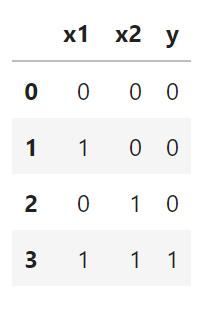
AND演算は「入力がどちらも1ならば1、それ以外ならば0」を返します。
ここで、DataFrameの各行0~3までをそれぞれ入力データとして見てみると、x1,x2は各データの特徴になります。
yはデータを受け取ったパーセプトロンに返してほしい出力値です。
このyの値と同じ値を返してくれれば、パーセプトロンでANDゲートを実装できたことになります。
パーセプトロンの実装
では、PythonでANDゲートを再現するパーセプトロンを実装しましょう。
パーセプトロンの最も簡単な実装では、w1,w2などのパラメータはプログラマが自分で値を与えます。
この値については、パーセプトロンの式(二元一次方程式)を手作業で解くことで与えられますね。
ここでは、w1とw2は0.5としました。
また、しきい値θについても決める必要があります。
ここでは0.7としてみましたが、これらの値は他にも適した組み合わせがあります。
考えてみてください。
def AND_gate(x1,x2):
w1,w2 = 0.5,0.5
theta = 0.7
tmp = w1*x1 + w2*x2
if tmp <= theta:
y = 0
else:
y = 1
return y
さて、このAND_gate関数が実際にANDゲートを再現できているかチェックしましょう。
すべての入力データの組み合わせに対して答えを出してみます。
print(AND_gate(0,0)) print(AND_gate(1,0)) print(AND_gate(0,1)) print(AND_gate(1,1))
[出力結果]
0 0 0 1
この値は最初に作ったANDゲートのデータフレームのy列と同じ値になっています。
これでパーセプトロンを使ったANDゲートの実装ができましたね!
バイアスの導入
バイアスを導入したパーセプトロン
さて、先程までのパーセプトロンでは、しきい値θという値が登場しました。
ですが、このθの値、wと同様にプログラマが変更するべきパラメータでした。
ここからは、このしきい値θをバイアス(bias)という値に置き換えたパーセプトロンを実装してみます。
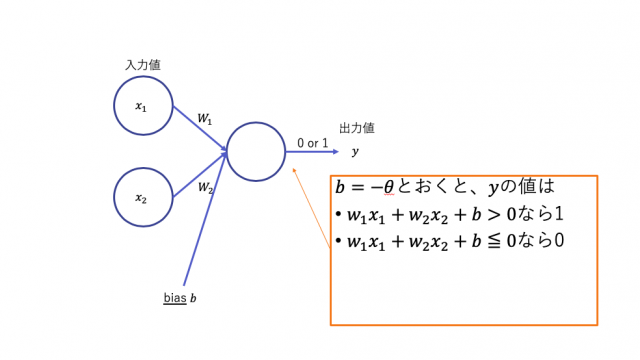
biasを式中ではbとしました。
このとき、b=-θと考えて式を変形すると、上のように右辺(不等式の右側)を0で統一できますね。
こっちのほうが見やすくて実装も考えやすいので、普通はこちらが使われます。
バイアスを導入したパーセプトロンの実装
では先程と同じ例題を、バイアスを使ったパーセプトロンで試してみましょう。
コードの修正点は
- thetaの部分がbになって値がマイナスになっている
- 条件式が0より大きいかどうかになっている
の二箇所です。
def AND_gate2(x1,x2):
w1,w2 = 0.5,0.5
b = -0.7
tmp = w1*x1 + w2*x2 + b
if tmp <= 0:
y = 0
else:
y = 1
return y
print(AND_gate2(0,0))
print(AND_gate2(1,0))
print(AND_gate2(0,1))
print(AND_gate2(1,1))
[出力結果]
0 0 0 1
正しく動作していますね。
単純パーセプトロンの限界
単純パーセプトロンで簡単なANDゲートの再現ができることがわかりました。
ここで紹介はしませんでしたが、この他にもORゲートやNANDゲートなどが実装できます。
さて、ではこの単純パーセプトロンを使えばすべての論理演算が実装できるのでしょうか?
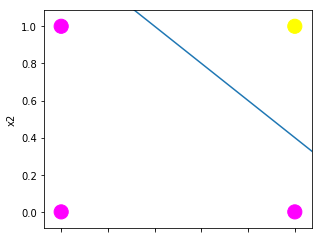
[ANDゲートのグラフ]
ANDゲートの例題で使った入力信号を二次元グラフにしました。
通常x軸があるところがx1軸、y軸があるところがx2軸、黄色がy=1, ピンクがy=0です。
青色の線は単純パーセプトロンがこれらのデータ点を分類するときに使っている境界線です。
このように、単純パーセプトロンでは直線を一本引いて境界線を決めています。
これで分類できる問題ならば分類が可能そうですが、以下のような問題ではどうでしょうか。

[XORゲートのグラフ]
このグラフでは、一本の直線で境界線を引くことができません。
このような問題の場合、境界線を一本しか引けない単純パーセプトロンでは再現することができませんね。
これが単純パーセプトロンの限界です。
これを克服するための方法にはいくつか方法がありますが、順当に考えると
「パーセプトロンを複数使って多層化する→多層パーセプトロン」
を考えるのが一般的です。
これについてはまた別の記事で!
まとめ
この記事では、単純パーセプトロンについて紹介し、理論と実装を見ていきました。
また別の記事で、単純パーセプトロンを拡張したアルゴリズムについて紹介していきます。
まずは単純パーセプトロンを理解して、ニューラルネットワークの世界に一歩踏み出しましょう!









