こんにちは!フリーランスエンジニア・ライターの平山です。
皆さんの中に、こんなお悩みの方はいないでしょうか?
「素数を判定するプログラムを組みたいのだけど、さっぱりわからない!」
「素数に興味があるのだけれど、プログラムで手軽に素数が判定できないものか。」
素数判定は、アルゴリズムをプログラムに落とし込むいい練習になります。
そのため、課題として使われることも多いものです。
そこで、この記事では
・素数の基礎
・様々な素数判定法の紹介
といった基礎的な内容から、
・試し割り法
・エラトステネスのふるい
・ライブラリ
それぞれを使った素数判定の実践までお伝えしていきます。
この機会に、古くて新しい素数の世界をのぞいてみましょう。
本記事を読む前に、Pythonがどんなプログラミング言語なのかをおさらいしておきたい人は次の記事を参考にしてください。
→ Pythonとは?特徴やできること、活用例をわかりやすく簡単に解説
なお、その他のPythonの記事についてはこちらにまとめています。
素数の基礎

まずは、素数について基本的な部分を見ていきましょう。
素数とは何か?
最初に素数とは何か?から始めていきます。
素数は一般に次のように定義されています。
1 より大きい自然数で、正の約数が 1 と自分自身のみであるもののことである。
引用:Wikipedia
URL:https://ja.wikipedia.org/wiki/%E7%B4%A0%E6%95%B0
大事なことは、約数が1と自分自身のみである、ということですね。
約数とは対象の数を割り切ることのできる整数のことです。
逆に1と自分自身以外に約数を持つ数を「合成数」といいます。
素数の定義は非常にシンプルです。
ところが、素数を簡単に算出できる公式は存在しません。
素数についての研究は2200年以上前から行われていた、と言われています。
それでも、まだまだわからないことがたくさんあるのです。
現代でも100万ドルの懸賞金がかかった未解決問題のひとつに素数をテーマにしたものがあります。
参考:ミレニアム懸賞問題
URL:https://ja.wikipedia.org/wiki/%E3%83%9F%E3%83%AC%E3%83%8B%E3%82%A2%E3%83%A0%E6%87%B8%E8%B3%9E%E5%95%8F%E9%A1%8C
また、インターネットの安全性は暗号理論に支えられています。
SSL/TLSなどの通信を暗号化する技術の基礎を支えているのは、実は素数なのです。
古くて最先端の問題。
それも素数の魅力の一つかもしれません。
素数を判定する方法
それでは、素数を判定する方法をいくつか紹介していきましょう。
前節の繰り返しになりますが、素数を簡単に求める公式は存在しません。
ですが、素数の性質を利用することでその数を判定することはできます。
例として、123は素数かどうかを判定してみましょう。
このとき、一番シンプルな方法として考えられるのが、次の方法です。
・123までのすべての整数で割ってみる。
素数の定義は「1と自分自身以外に約数を持たない」というものでした。
これを利用して「自身以外で割り算を行い、素数であることを証明しよう」という考え方です。
最悪、素数にたどり着くまでに122回割り算をしなければなりませんが、確実に素数判定ができます。
この考え方を使った方法を「試し割り法」と呼びます。
考え方がわかりやすいことが、一番のメリットですね。
デメリットとしては、計算に非常に時間がかかることです。
約数が比較的小さい数であれば、すぐに合成数と判断できます。
ですが、桁数が大きくなると、もはや一般には手に負えないレベルの計算時間が必要になってきます。
試し割り法に限らず、素数の判定は計算時間との戦いとも言えるでしょう。
そこで、計算時間を少しでも短縮するために、2種類のアプローチがあります。
・決定的素数判定法
計算を少しでも効率化して、素数を確実に判定することに重点を置く考え方。
- 試し割り法
- エラトステネスのふるい
- AKS素数判定法
などがある。
・確率的素数判定法
確率的アルゴリズムを使って、対象の数を合成数か「素数である確率の高い数」に分類する方法
- フェルマーテスト
- ミラー–ラビン素数判定法
などがある。
動作が高速な点がメリット。
確率的素数判定法の補足
確率的素数判定法について、頭に疑問符が浮かんだ方も多いのではないでしょうか?
合成数はわかるとして、「素数である確率の高い数」とはなんなんだ、と。
ここで理論の詳細に立ち入ることはしませんが、おおよそ次のような方法です。
- 素数pと互いに素な整数aに対して成り立つフェルマーの小定理と言うものがある。
- この定理の対偶を取ることで対象の数pが合成数かどうかが判定できる。
- 様々なaをランダムで選び2.を繰り返すことで合成数であるかどうかを検証する。
これが確率的素数判定法の考え方になります。
3.の部分を何回も繰り返すことで対象の数が素数である確率が高まるのは直感的に理解できるかと思います。
ですが、残念なことにテストを何回繰り返しても絶対合格してしまう「合成数」も存在します。
この数はカーマイケル数と呼ばれ、無限に存在することが知られています。
そのため、確率的素数判定法は素数である確率が高いとしか言えないわけです。
ところが、2016年にカーマイケル数の導出方法がみつかったかもしれない、というニュースが流れました。
URL:https://edition.cnn.com/2016/07/17/asia/china-migrant-worker-good-will-hunting/index.html
まだ証明されたわけではないようですが、もし正しいことがわかれば大発見間違いなしですね!
次の章からは決定的素数判定法のアルゴリズムをPythonに実装してみましょう。
素数判定法その1・試し割り法
まずは前章で紹介した試し割り法を実装しましょう。
試し割り法を使って判定する
さっそく試し割り法を実装!と行きたいところですが、その前に少しだけ。
試し割り法の概要は前章で紹介しましたが、そこで次の問題点を指摘しました。
「計算量が多いため、計算に時間がかかる。」
そこで、本節ではすこしでも計算量を減らして効率化することを考えてみましょう。
まず考えられるのが次の点です。
「わざわざ対象の数-1の数まで割らなければならないのか?」
前の具体例では123が素数であるかどうかを求めるためには、122まで割ってみればいい、という説明をしました。
ですが、冷静に考えてみれば、123が122や120で割り切れることはありえませんよね。
割るべき数はどんなに多くても62を超えることはないはずです。(123 < 62*2)
そして、次の考え方を使うともっと割るべき数の上限がさがります。
任意の整数nについて、試し割り法を実行する。
nが何らかの数aで割り切れたとする。
このとき n = a * b を満たす整数 b が存在する。
b < a の場合、すでにb 自身、もしくは b の約数で試し割りを行っているはずである。
そのため、aについては試し割りを行わなくて良い。
n のすべての約数について同様に考えていくと、√n まで試し割りをすることで十分である。
(b < a のとき、b の最大値 ≦ a の最小値 ≦ √nのため。)
このことから、試し割りの上限は√123 = 11.09… つまり、11までで良いことがわかりました。
かなり計算量が減りましたね!
次の節では実際にPythonで試し割り法を実装していきましょう。
試し割り法を実装する
それでは、さっそく実装に移ります。
まずはソースの全体像を御覧ください。
import math
number = 123
def trial_division(target):
dest = int(math.sqrt(target))
for i in range(2,dest):
if target % i == 0:
print(str(target) + 'は合成数!')
return
print(str(target) + 'は素数!')
trial_division(number)
やっていることは非常に単純です。
3行目で判定したい数を number 変数に代入
6行目でtarget引数の平方根をとり、それを整数化したものを dest変数に代入
8行目からのfor文でtarget の商を2からdestまでとり、割り切れたものは「合成数!」と表示
最後まで割り切れなかった場合、素数と判定して表示
今までに説明してきたことが全て盛り込まれていますね。
次の章ではさらなる効率化を目指して、エラトステネスのふるいを実装します。
素数判定法その2・エラトステネスのふるい
本章では前節で実装した試し割り法を更に効率化するため、「エラトステネスのふるい」という考え方を導入します。
エラトステネスのふるいとは?
まずはエラトステネスのふるいとはなにか?というところから見ていきましょう。
エラトステネスは、紀元前200年頃にエジプトで活躍したギリシャ人の学者です。
多方面で活躍された方ですが、特に有名なのが次の2点。
- エラトステネスのふるいを考案したこと
- 地球の大きさを初めて測定したこと
ヨーロッパでは16世紀にコペルニクスが登場するまで地動説が信じられていました。
その1700年以上前に地球を球体と考えて、その大きさを測定してしまった人物がいたのですから驚きですね。
さて、もう一つの功績である「エラトステネスのふるい」に話を戻しましょう。
「ふるい」は漢字で「篩」と書かれることもあります。
この方法は、まるでふるいにかけるように合成数を排除していき、最後に素数の一覧を得るところに特徴があります。
具体例として、100までの素数をエラトステネスのふるいをつかって求めてみましょう。
まず、下のように1を除外した2から100までの整数を表にします。
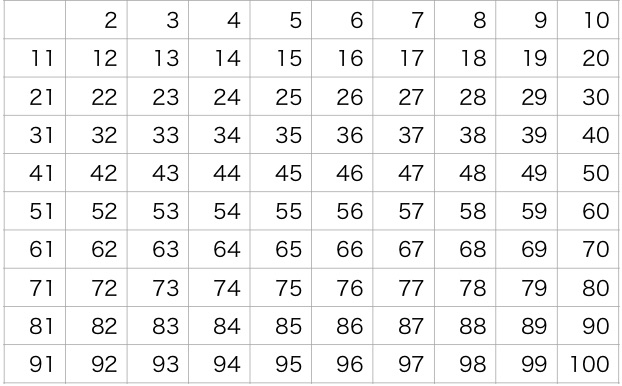
1は素数の定義から、素数ではないことが明らかなので最初から除外しています。
つぎに、2について調べます。
2は自身と1以外割り切れる数がありません。
よって素数です。
また、2の倍数はすべて合成数です。
そのため、表から2の倍数をふるい落とします。
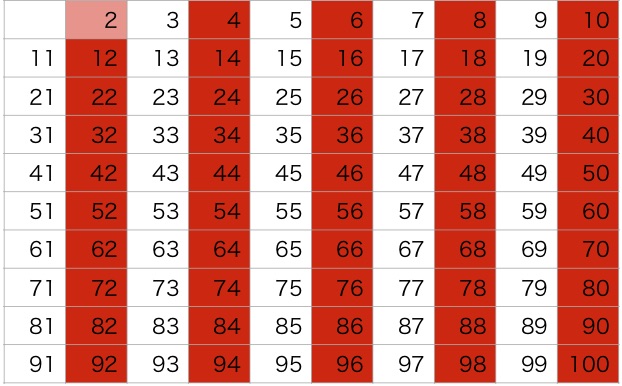
その結果下の表が得られました。
この操作がふるいで不純物を取り除くようであるため、エラトステネスのふるいと呼ばれています。
つづいて、2の次の数でなおかつ表に残っている3に着目します。
3は自身と1以外で割り切れないため、素数です。
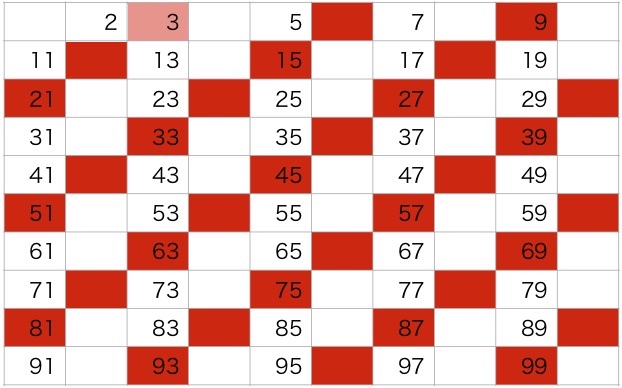
そこで、3の倍数をふるい落とします。
つぎに、3の次の数で表に残っている5に着目します。
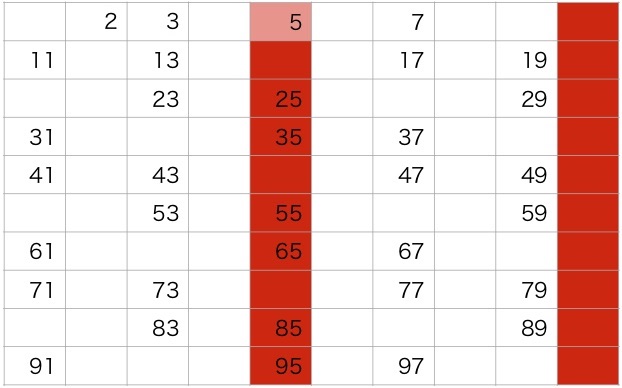
同様に5は素数であり、5の倍数をふるい落とします。
この手続を√100 = 10 まで繰り返します。(なぜ√100まででいいのかは前節をご参照ください)


7の倍数をふるい落とします。
この時点で次の数が10を超えたので終了します。
結果、ふるい落とされなかった数が素数となります。
シンプルな考え方ですが、確実に100までの素数が求められましたね。
それではこれをPythonで実装してみましょう。
エラトステネスのふるいを実装する
エラトステネスのふるいの実装に移ります。
ソースは次のようになります。
import math
serach_number = 100
def sieve_of_eratosthenes(target):
dest = int(math.sqrt(target))
target_list = list(range(2, target + 1))
prime_list = []
while True:
num_min = min(target_list)
if num_min >= dest:
prime_list.extend(target_list)
break
prime_list.append(num_min)
i = 0
while True:
if i >= len(target_list):
break
elif target_list[i] % num_min == 0:
target_list.pop(i)
i += 1
print(prime_list)
sieve_of_eratosthenes(serach_number)
外側のwhileループはnum_min、つまりふるいにかける数が10を超えた段階でbreak。
残りを素数のリストに入れています。
一方内側はループ変数 i がtarget_listの大きさを超えたらbreakするようにしてあります。
その他の部分は今までの説明をそのまま実装した形になっています。
なお、高速化は一切念頭に置いていないため、7桁程度の素数を判定するのがこのプログラムの限界です。
7桁で2分程度かかるので、それ以上の桁を計算する場合、お覚悟を。
エラトステネスのふるいの高速化については、多くの方が実践されているので、興味のある方はぜひ検索してみてください。
きっと、思いもよらないPythonの使い方に出会えることでしょう。
最後にライブラリをつかった簡単な素数の判定・列挙法をお伝えします。
ライブラリを使って簡単に判定・列挙する
前章まででシンプルな素数の判定法を2つお伝えしました。
この章では SymPy パッケージを使って、より簡単に素数を判定・列挙する方法を紹介します。
SymPyとは?
SymPy は数式を記号的に処理するためのパッケージです。
基本的な四則演算から多項式、因数分解、ベクトル、微分方程式、統計や暗号などなど。
非常に幅広いジャンルに対応できるパッケージになっています。
今回はNtheoryクラスを使って素数を扱う方法を見ていきましょう。
ちなみに、このクラスはエラトステネスのふるいを使って素数を得ています。
そのため、計算速度はそこまで早くありません。
10桁を超えたあたりから計算に非常に時間がかかるようになります。
大きな素数を検証するときは特に注意しましょう。
それではさっそく、パッケージのインストールから始めましょう。
SymPyはpipで提供されているため、以下のコマンドで簡単にインストールできます。
pip install sympy
無事インストールができましたか?
つづいて素数に関係するメソッドを見ていきましょう。
まずは、prime(n)
これはn番目の素数を返します。
from sympy import prime print(prime(10)) # 結果 29
次にprimerange(a,b)
これは整数aからbまでの間の素数をすべて求める関数です。
from sympy import sieve print([i for i in sieve.primerange(7,23)]) # 結果 [7, 11, 13, 17, 19]
nextprime(n,i = 1) これは、n より大きい i 番目の素数を返します。
i はデフォルトで1に設定されています。
from sympy import nextprime print(nextprime(123)) # 結果 127
最後に、isprime(n)
これは n が素数かどうかを判定します。
注意点が1つ。
2の64乗までの数(およそ19桁)までは決定的素数として求められます。
ですが、それ以降は疑似素数が含まれる可能性がわずかながら存在します。
from sympy import isprime print(isprime(67280421310721)) # 結果 True
SymPy は他にもランダムな素数を返す randprime や n 番目の合成数を返す composite などなど、面白い関数がたくさんあります。
興味のある方はぜひ公式ドキュメントを御覧ください。
URL:https://docs.sympy.org/latest/modules/ntheory.html
素数の生成・判定プログラムを実装!まとめ
いかがでしたか?
今回はPythonを使って以下のことをお伝えしました。
- 素数の基礎
- 試し割り法・エラトステネスのふるいによる素数の求め方
- パッケージを使った素数の求め方
素数は数学的に重要であるとともに、暗号理論の基礎になるなど、現代社会では欠かせないものになっています。
もし素数についていろいろ調べたくなったら、この記事を振り返ってみてください。









