こんにちは!フリーランスエンジニア・ライターの平山です。
皆さんの中には微分方程式について、こんなお悩みをお持ちの方もいるのではないでしょうか?
「微分方程式を数値解析してみたい!でも、やり方がわからない・・・」
「Pythonだと簡単に数値解析やシミュレーションができると聞いたんだけど、方法がよくわからない」
Pythonは科学計算を得意として発展してきた歴史があります。
そのため、微分方程式の数値解析は得意分野のひとつでもあるのです。
今回はSciPyというパッケージを使い、簡単な関数からカオスと呼ばれる複雑なものまで、解き方を紹介します。
解析結果をアニメーションで見る方法もお伝えしまので、式だけでは見えてこなかった世界が発見できるかもしれません。
それでは、Pythonを使った数値解析の世界に一歩踏み出しましょう!
本記事を読む前に、Pythonがどんなプログラミング言語なのかをおさらいしておきたい人は次の記事を参考にしてください。
→ Pythonとは?特徴やできること、活用例をわかりやすく簡単に解説
なお、その他のPythonの記事についてはこちらにまとめています。
SciPyを使った微分方程式の解き方
それではSciPyを使って微分方程式を解く方法を見ていきましょう。
SciPyをインストールする
まずは、SciPyのインストールからです。
SciPyは前提としてnumpyが必須です。
また、結果をアニメーションで表現するためにはmatplotlibなどいろいろと必要になります。
そのため、公式が推奨しているパッケージの一括インストールコマンドを使用しましょう。
参照 https://www.SciPy.org/install.html
python -m pip install --user numpy SciPy matplotlib ipython jupyter pandas sympy nose
たくさんのパッケージをインストールするため、そこそこ時間がかかります。
なお、Anaconda環境を使っている方は最初からすべてインストール済みのため、この工程はスキップできます。
Anacondaについて詳しくはこちらの記事をご覧ください。


SciPyの特徴は次の説明に集約されます。
プログラミング数学、科学、工学のための数値解析ソフトウェアである。
URL:https://ja.wikipedia.org/wiki/SciPy
そのため、微分方程式以外にもいろいろと計算することができます。
微分、積分、フーリエ変換、統計、などなど。
興味のある方はぜひリファレンスをご覧ください。
SciPyで簡単な微分方程式を解いてみる
インストールができましたので、さっそく簡単な微分方程式をといてみましょう。
以下の式をSciPyをつかって数値的に解いていきます。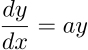
この微分方程式、解析的に解くことはできますが、数値解法の練習ということでお付き合いください。
まずは必要なパッケージをインポートします。
import numpy as np from SciPy.integrate import odeint import matplotlib.pyplot as plt
SciPyはnumpyを前提とするので、numpy
微分方程式を解くための積分器として、odeint
結果をグラフで表示するために、matplotlib.pyplot
をインポートしました。
odeintは1階の常微分方程式を解くのに有効な積分器です。
関数の硬さによらず1階の常微分方程式を数値計算できます。
そのため、1手目としてodeintを使うのが良いでしょう。
odeintがだめな場合はodeというより一般的な積分器も用意されています。
こちらは計算方法を指定できるので、ルンゲクッタ法など、特定の解法で解きたい人にはうれしいパッケージです。
つづいて、微分方程式として解くための関数と定数を定義します。
def func(y, x, a):
dydx = a*y
return dydx
a = 1
y0 = 1
x = np.arange(0, 3, 0.01)
関数にはdydx、つまり先程の微分方程式を記述して、返り値にdydxを設定します。
その下で式中の定数a,解の初期値y0,yの変数xをそれぞれ設定しています。
そして今回の山場、微分方程式の数値解を求める関数、odeintに各種引数を代入していきます。
y = odeint(func, y0, x, args=(a,))
引数は、対象の微分方程式、解の初期値、各種定数、の順に代入します。
argsパラメータは値をタプルで取ることに注意が必要です。
パラメータが1つであっても例のように後ろにカンマを付けてタプル表記で代入しましょう。
たったこれだけで、微分方程式の数値解を求めることができます。
あとは求めた解を図に表すだけです。
plt.plot(x, y, label= 'exp') plt.legend() plt.show()
plt.plotで図のセッティングを行います。
- 2次元のプロットの場合、plt.plotを使います。引数は、横軸、縦軸、凡例のラベル、に対応します。
- plt.legend()で凡例をグラフに表示できます。
- 最後にplt.show()を入力することで、グラフが表示できます。
下のようなグラフが出ましたか?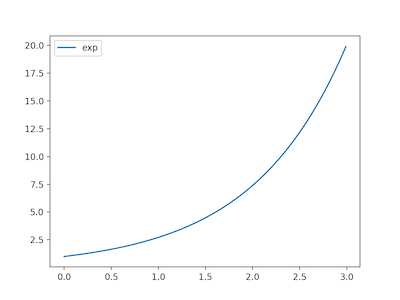
これは、ご存知のかたも多いかもしれませんが、指数関数 y = e^x のグラフになります。
無事、微分方程式を解いてグラフまで表示できました!
ここまでのコードをまとめます。
import numpy as np
from SciPy.integrate import odeint
import matplotlib.pyplot as plt
def func(y, x, a):
dydx = a*y
return dydx
a = 1
y0 = 1
x = np.arange(0, 3, 0.01)
y = odeint(func, y0, x, args=(a,))
plt.plot(x, y, label= 'exp')
plt.legend()
plt.show()
今度は時間変化でアニメーションするグラフを作ってみましょう。
解析結果をアニメーションで見る
この章ではmatplotlibをつかって、関数をアニメーションさせる方法を見ていきます。
matplotlibの詳しい説明が必要な方は以下の記事を参照ください。


単振り子の微分方程式をつくる
アニメーションさせる関数として、高校物理でお馴染みの単振り子を使いましょう。
こんな感じのものでしたね。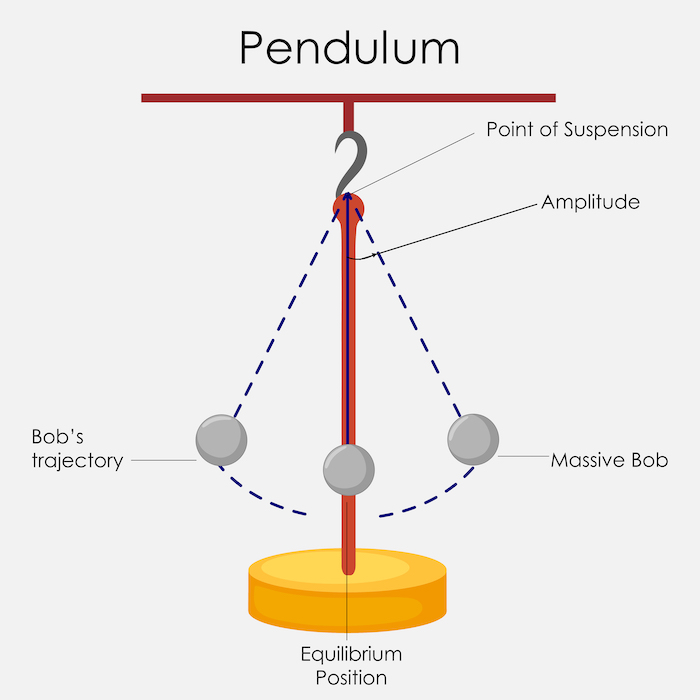
解析する微分方程式は以下の通りとなります。
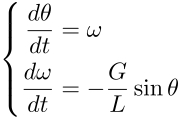
細かい理屈などはWikipediaなどをご参考ください。
では、早速コードをみていきます。
import matplotlib.pyplot as plt import numpy as np from numpy import sin, cos from matplotlib.animation import FuncAnimation from SciPy.integrate import odeint
インポートすべきものは前章のものに加えて
numpyから三角関数
関数をアニメーションさせるためにmatplotlib.animationのFuncAnimation
を追加しました。
つづいて、微分方程式を関数で表現します。
定数と合わせて次のように書きます。
def func(state, t):
dydt = np.zeros_like(state)
dydt[0] = state[1]
dydt[1] = -(G/L)*sin(state[0])
return dydt
G = 9.8 # 重力加速度
L = 1 # 振り子の長さ
th1 = 30.0 # 角度の初期値[deg]
w1 = 0.0 # 角速度の初期値[deg]
# 初期状態
state = np.radians([th1, w1])
前より少し複雑になりましたね。
G、L は基本的な定数ということで問題ないでしょう。
th1 , w1 も振り子の問題を解いたことのある方にはおなじみの、角度と角速度の初期値です。
np.radians() をつかって、角度をラジアンに変換しているのもそこまで難しい操作ではありません。
おそらく一番違和感を感じるのは関数定義のdydt = np.zeros_like(state)から始まる部分ではないでしょうか?
これは何をしたいのかというと、
- まず、角度と角速度のリストを作る(state = np.radians([th1, w1]))
- stateと同じ形のゼロ埋めされたリストdydt = [0, 0] を作る(dydt = np.zeros_like(state))
- dydtのインデックス0番目に角度の微分、つまり角速度を代入(dydt[0] = state[1])
- dydtのインデックス1番目に角速度の微分、つまり振り子の運動方程式を代入(dydt[1] = -(G/L)*sin(state[0]))
ということをやっています。
要するに下の式をそのまま関数定義に書き換えているわけです。
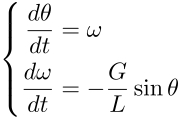
微分方程式をodeintが解釈できる形に変換するのは、少々慣れが必要です。
ですが、わかってしまえば大したことはやっていないので、ぜひ頑張って挑戦してみてください。
つづいて、微分方程式を実際に解いていきましょう。
dt = 0.05 t = np.arange(0.0, 20, dt) sol = odeint(func, state, t) theta = sol[:, 0] x = L * sin(theta) y = - L * cos(theta)
やることは先程とあまり変わりません。
パラメータtを0から20まで、0.05刻みで動かしたtというリストをつくります。
odeint()に先程のfunc,state,tを代入します。
結果、角度と角速度のリスト、sol = [th,w]を得ました。
そこから角度のみを取り出し、x-y座標に変換しています。
結果をアニメーションで表現する
最後に計算結果をアニメーションで表示しましょう。
fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L, L), ylim=(-L, L))
ax.set_aspect('equal')
ax.grid()
line, = ax.plot([], [], 'o-', lw=2)
def animate(i):
thisx = [0, x[i]]
thisy = [0, y[i]]
line.set_data(thisx, thisy)
return line,
ani = FuncAnimation(fig, animate, frames=np.arange(0, len(t)),interval=25, blit = True)
plt.show()
先程の例とは異なり、最初にfigureインスタンスを生成しています。
こうすることで、グラフに対してより詳細な設定が可能になります。
逆に、figureインスタンスを生成するといろいろ設定をしなくてはならず面倒とも言えます。
とりあえずグラフにしたい場合、あえてインスタンス化しないことも実用上よくあります。
状況に応じて使い分けるのがよいでしょう。
さて、インスタンスを生成した場合、まずは軸を設定しなくてはいけません。
それが、add_subplot()メソッドです。
第1引数の「111」は、複数のグラフを同時に描写したり重ねたりする場合に調整が必要になる部分です。
今回のようにひとつのグラフのみを扱う場合、111と覚えておいて問題ないでしょう。
その他のパラメータ、メソッドは
- autoscale_on=False,で軸の自動スケーリングを止めています。
- xlim=(-L, L), ylim=(-L, L)ではグラフの大きさを制限しています。振り子が入り切る適切な大きさとして設定します。
- ax.set_aspect(‘equal’)で縦横比を固定します。縦横のバランスが等しいほうが見栄えが良いためです。
- ax.grid()で格子線を描画します。
- line, = ax.plot([], [], ‘o-‘, lw=2)はこの時点では位置座標を持たない線を設定しています。このlineに次々と座標を代入しながら描画することで振り子のアニメーションを実現します。
- ‘o-‘は端点と線の形、 lw=2は先の太さを設定するパラメータになります。
最後にアニメーションの設定を行います。
ソースとは前後しますが、FuncAnimationの説明からいきましょう。
関数をアニメーションさせるには、名前の通り、matplotlib.animation の FuncAnimationを使います。
FuncAnimationの引数は、
fig:先程設定したベースとなるグラフ
animate:アニメーションさせたい関数
を代入してあげれば最低限動かすことができます。
ただ、今回は時間tを20までしか定義していないので、途中で動作が止まりエラーとなってしまいます。
そのため、アニメーションさせるフレーム数を制限するframes=パラメータをつかいました。
interval , blit は本来設定しなくてもいいパラメータですが、動作の滑らかさのために指定しています。
animate関数は、引数に時間をもち、図を描画する機能を持つように作ります。
そして、かならずFuncAnimationの前に定義しなくてはいけません。
この例では時間iでの振り子の始点と終点の座標をthisx 、thisy に代入し、set_data() を使ってline を描画する機能を持ちます。
さあ、すべての準備ができました。
あとは、plt.show()コマンドを最後に入れて、ファイルを実行してみましょう。
import matplotlib.pyplot as plt
import numpy as np
from SciPy.integrate import odeint
from numpy import sin, cos, pi
from matplotlib.animation import FuncAnimation
def func(state, t):
dydt = np.zeros_like(state)
dydt[0] = state[1]
dydt[1] = -(G/L)*sin(state[0])
return dydt
G = 9.8 # 重力加速度
L = 1 # 振り子の長さ
th1 = 30.0 # 角度の初期値[deg]
w1 = 0.0 # 角速度の初期値[deg]
# 初期状態
state = np.radians([th1, w1])
dt = 0.05
t = np.arange(0.0, 20, dt)
sol = odeint(func, state, t)
theta = sol[:, 0]
x = L * sin(theta)
y = - L * cos(theta)
fig = plt.figure()
ax = fig.add_subplot(111, autoscale_on=False, xlim=(-L, L), ylim=(-L, L))
ax.set_aspect('equal')
ax.grid()
line, = ax.plot([], [], 'o-', lw=2)
def animate(i):
thisx = [0, x[i]]
thisy = [0, y[i]]
line.set_data(thisx, thisy)
return line,
ani = FuncAnimation(fig, animate, frames=np.arange(0, len(t)),interval=25, blit = True)
plt.show()
このようなアニメーションが表示できましたか?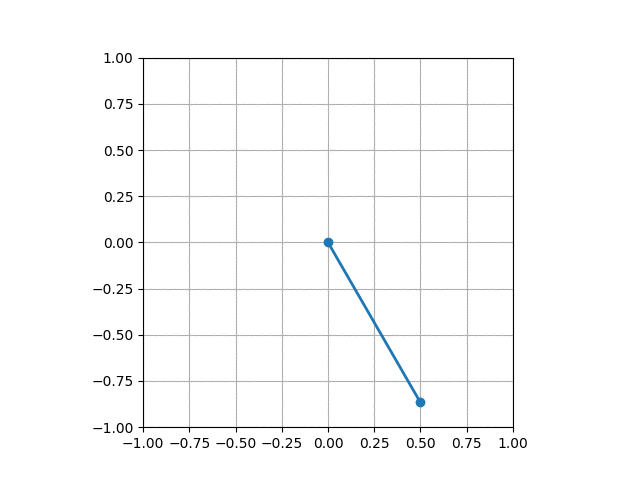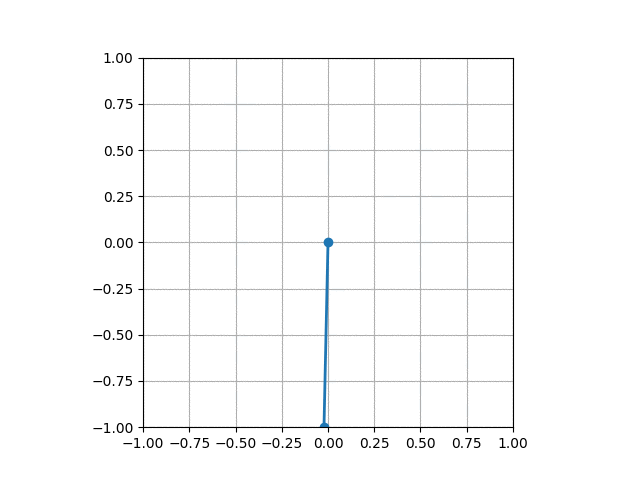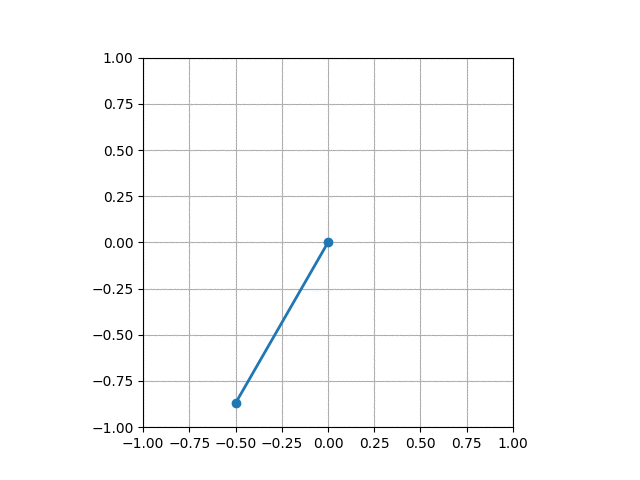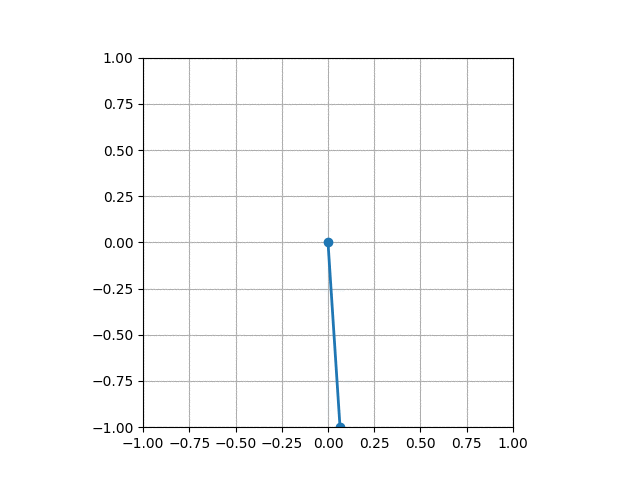
二重振り子を数値的に解く!
それでは最後に応用編として、先程の振り子の先に更に振り子を取り付けた二重振り子について扱ってみましょう。
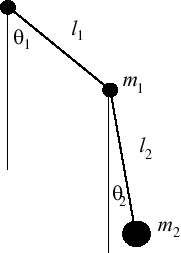
ぱっと見簡単に解けそうな感じですが、実はこの振り子、解析的に解けないんです。
この振り子を動かすと、非常に複雑で、非周期的な運動になるのです。
この性質を「カオス」と呼びます。
そんなカオスを手軽にシミュレーションしてみよう、というのが本章の趣旨になります。
とりあえず、微分方程式を書いてみましょう。
運動方程式は下記のようになります。
時間微分をドットで表していることに注意してください。
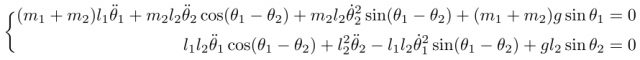
これを変形することで次の一階の微分方程式を得ます。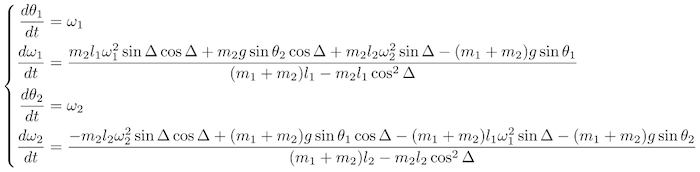
ただし![]()
サラリと書きましたが、結構メンドウな計算なので、やる気のある方はぜひ解析力学の教科書とにらめっこしてください。
さて、1階の微分方程式さえ求まってしまえばこっちのものです。
あとは今までと全く同じ手順で数値解析からアニメーションまでできてしまうからです。
さらにありがたいことに、matplotlibが公式で二重振り子のソースを提供してくれています。
ありがたく使わせていただきましょう。
ソースの全文が以下になります。
from numpy import sin, cos
import numpy as np
import matplotlib.pyplot as plt
import SciPy.integrate as integrate
import matplotlib.animation as animation
G = 9.8 # acceleration due to gravity, in m/s^2
L1 = 1.0 # length of pendulum 1 in m
L2 = 1.0 # length of pendulum 2 in m
M1 = 1.0 # mass of pendulum 1 in kg
M2 = 1.0 # mass of pendulum 2 in kg
def derivs(state, t):
dydx = np.zeros_like(state)
dydx[0] = state[1]
del_ = state[2] - state[0]
den1 = (M1 + M2)*L1 - M2*L1*cos(del_)*cos(del_)
dydx[1] = (M2*L1*state[1]*state[1]*sin(del_)*cos(del_) +
M2*G*sin(state[2])*cos(del_) +
M2*L2*state[3]*state[3]*sin(del_) -
(M1 + M2)*G*sin(state[0]))/den1
dydx[2] = state[3]
den2 = (L2/L1)*den1
dydx[3] = (-M2*L2*state[3]*state[3]*sin(del_)*cos(del_) +
(M1 + M2)*G*sin(state[0])*cos(del_) -
(M1 + M2)*L1*state[1]*state[1]*sin(del_) -
(M1 + M2)*G*sin(state[2]))/den2
return dydx
# create a time array from 0..100 sampled at 0.05 second steps
dt = 0.05
t = np.arange(0.0, 20, dt)
# th1 and t
are the initial angles (degrees)
# w10 and w20 are the initial angular velocities (degrees per second) th1 = 120.0 w1 = 0.0 t
= -10.0
w2 = 0.0 # initial state state = np.radians([th1, w1, th2, w2]) # integrate your ODE using SciPy.integrate. y = integrate.odeint(derivs, state, t) x1 = L1*sin(y[:, 0]) # リストの0番目、θ1を取り出しています。 y1 = -L1*cos(y[:, 0]) x2 = L2*sin(y[:, 2]) + x1# リストの2番目、θ2を取り出しています。 y2 = -L2*cos(y[:, 2]) + y1 fig = plt.figure() ax = fig.add_subplot(111, autoscale_on=False, xlim=(-2, 2), ylim=(-2, 2)) ax.set_aspect(‘equal’) ax.grid() line, = ax.plot([], [], ‘o-‘, lw=2) # タイマーを表示するために追加されました time_template = ‘time = %.1fs’ time_text = ax.text(0.05, 0.9, ”, transform=ax.transAxes) def init(): line.set_data([], []) # これもタイマー用の初期化 time_text.set_text(”) return line, time_text def animate(i): thisx = [0, x1[i], x2[i]] thisy = [0, y1[i], y2[i]] line.set_data(thisx, thisy) # タイマー更新用 time_text.set_text(time_template % (i*dt)) return line, time_text ani = animation.FuncAnimation(fig, animate, np.arange(1, len(y)), interval=25, blit=True, init_func=init) plt.show()
なかなかの分量なので、尻込みしてしまうかもしれませんが、安心してください。
やっていることは2章の単振り子とほとんど同じです。
インポートしているパッケージはまったく一緒。
関数定義は二重振り子のため、複雑にはなりました。
ですが、微分方程式を解くのは相変わらずodeintですし、アニメーションは時間表示機能がついただけです。
ぜひ実際に動かしてみて、自分の手でカオスを体感してください。
想像以上に変な動きになることうけあいです。
微分方程式をSciPyで解く・まとめ
いかがでしたか?
今回はSciPyをつかった微分方程式の数値解法を学びました。
一昔前は研究室の大型コンピュータでもないとできなかったシミュレーションが、今ではものの数秒でパソコンでできるようになりました。
すごい時代になったものです。
みなさんもぜひいろいろな微分方程式を数値解析してみてください。
そこからまた新しい発見が生まれるかもしれません。
もし、数値解法の手順を忘れてしまったら、またこの記事を見に来てくださいね。









