こんにちは、ライターのアキヒロです。
PythonではNumpyを使うことで逆行列の計算が可能となります。
しかし、初心者にとっては
「逆行列を簡単に計算するにはどうしたらいいんだろう」
「そもそも逆行列って何?」
などの悩みを抱えている方も多いのではないでしょうか?
そこで、この記事ではPythonを使って逆行列を計算する方法を、以下の内容で説明します!
【基礎】逆行列とは何か
【基礎】逆行列を計算する方法
【発展】逆行列の検算方法
逆行列についてわかりやすく説明していますので、ぜひ参考にしてください!
本記事を読む前に、Pythonがどんなプログラミング言語なのかをおさらいしておきたい人は次の記事を参考にしてください。
→ Pythonとは?特徴やできること、活用例をわかりやすく簡単に解説
なお、その他のPythonの記事についてはこちらにまとめています。
逆行列とは?
Pythonでの逆行列の実装方法を解説する前に、逆行列とは何かを簡単に説明します。
逆行列とは、正則行列と掛けることで単位行列になる行列のことです。
単位行列とは対角成分が1で、それ以外が0の行列のことです。
行列A、逆行列A^(-1)、単位行列Eを式で表すと以下のようになります。
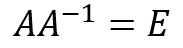
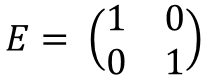
2次の正方行列では逆行列は以下のように求められます。
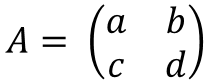
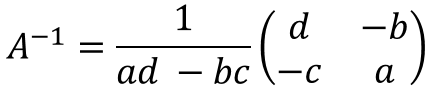
Numpyで逆行列を計算してみよう
それでは、実際に実装を見ていきましょう!
行列を定義する
最初に行列を変数matrixとして定義します。
matrix = [[1, 2],[3, 4]]
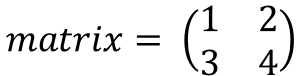
逆行列を求める
次にmatrixをもとに逆行列を求めるのですが、そのためにはNumpyライブラリのlinalg.invメソッドを使います!
Numpyライブラリを使うのでプログラムの最初にNumpyを読み込むためのインポート文を書きましょう。
import numpy as np
では逆行列を取得します。
逆行列を変数matrix_invとして、linalg.invメソッドで求めます。
matrix_inv = np.linalg.inv(matrix)
コードまとめ
最後に行列と逆行列を表示するためのコードを記述します。
ここまでをまとめたコードと実行結果です。
import numpy as np # 1.行列を定義 matrix = [[1, 2],[3, 4]] # 2.逆行列を取得 matrix_inv = np.linalg.inv(matrix) # 3.表示 print(matrix) print(matrix_inv)
【実行結果】
[[1, 2], [3, 4]] [[-2. 1. ] [ 1.5 -0.5]]
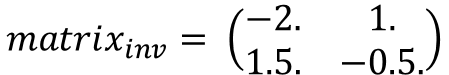
逆行列の計算が正しいかどうか調べよう
逆行列の性質を利用して検算を行ってみます。
行列と逆行列から単位行列を求める
先程の結果が本当に正しいのかどうかを調べてみましょう。
逆行列と行列の積をとると単位行列になります。
そこで実際に単位行列になるかどうか見てみましょう。
print(np.dot(matrix, matrix_inv))
np.dot()を使って行列の積を求めました。
【実行結果】
[[1.00000000e+00 1.11022302e-16] [0.00000000e+00 1.00000000e+00]]
思い通りの結果にならなかった原因
本来であれば
[[1 0]
[0 1]]
という結果が欲しかったのですが、全く異なる値が表示されています。
実は1.11022302e-16はほぼ0という値なので、近似的に単位行列が求められています。
逆行列の計算は一般的に、そのまま計算しようとすると誤差が大きく出てしまうことのある処理です。そのため近似的には単位行列になりますが、誤差が結果として表れています。
まとめ
今回はPythonのNumpyライブラリを使って逆行列を計算する方法を解説しました!
プログラミングで行列計算できれば機械学習などの分野で広く役立ちます。
ぜひマスターして行列をうまく求められるようになりましょう!









