この記事ではNumPyの紹介を行います。
機械学習やAIプログラムでは、非常に膨大な計算を行います。
そんな計算を効率的に行うためのライブラリがNumPyです。
この記事では
- NumPyとは
- 四則演算
- データの特徴を捉える値を計算
などの基本的な内容から
- 内積と外積
などの応用的な内容まで解説していきます!
NumPyは機械学習プログラミングで非常に重要なライブラリです。
この記事でNumPyに入門しちゃいましょう!
NumPyとは
高速に行列計算ができるNumPy
NumPyはPythonの行列計算ライブラリです。
実はPythonは他のプログラミング言語と比べてあまり速く計算ができません。
ではどうやってAIプログラミングなどの重い計算をやっているのかというと、実はこのNumPyに計算をしてもらっているんです。
NumPyはC/C++、Fortranなどの高速に動作する言語で実装されていて、Pythonから簡単に使うことができます。
このライブラリは現在の機械学習・ディープラーニングなどのAI技術のプログラムには必要不可欠なツールであり、AIプログラミングを行うために是非覚えておきたいツールです!
インストール方法
Anacondaを使ってPython環境を作ったならば、既にNumPyはインストールされています。
ちなみに、Anaconda環境でNumPyを手動インストールする時は、
conda install numpy
他の方法でPython環境を作って、NumPyをインストールする時は、
pip install numpy
でインストールできます。
NumPyの使い方

このセクションでは、NumPyを使った簡単な行列演算にチャレンジしましょう!
まずは準備として、NumPyをimportします。
NumPyは慣例としてnpというニックネームをつけますよ。
import numpy as np a = np.arange(6) a = a.reshape(2,3) b = np.arange(6,12) np.random.shuffle(b) b = b.reshape(2,3)
このプログラムでは、aとbというサンプル行列を作ります。
★ヒント
np.arrange(x,y)
> xからy-1までの要素を持った整数(int)型のベクトルを作ります。
z.reshape(x,y)
> zをx,y行列に変形します。
np.random.shuffle(x)
> xをランダムに並び替えます。
この操作によってaとbは以下のような値を持ちます。
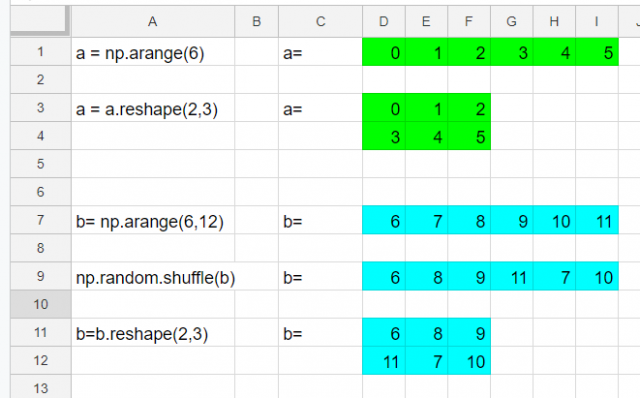
ではこれらを使って行列の計算をやってみましょう。
四則演算
演算子( + – * /など)を使った行列同士の計算は、要素同士の計算になります。
この解説でわかった人はOKです。次へ進んでください。
ストンとこなかった人は、謎の演算子★を使った例題、result=a★bを考えましょう。
この計算をしたとき、numpyは下のような動きをします。
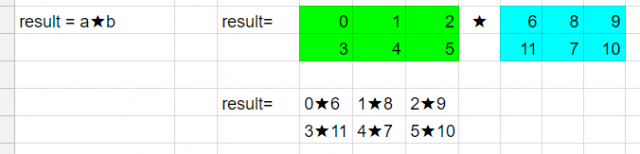
要素同士の計算とはこういうことです。
わかりましたか?
わかったら次へ。ストンとこなかった人は下の例題を手で計算してみましょう!
加算(足し算)
result = a+b
# 結果
array([[ 6, 9, 11],
[14, 11, 15]])
減算(引き算)
result = a-b
# 結果
array([[-6, -7, -7],
[-8, -3, -5]])
乗算(掛け算)
result = a*b
# 結果
array([[ 0, 8, 18],
[33, 28, 50]])
除算(割り算)
result = a/b
# 結果
array([[0. , 0.125 , 0.22222222],
[0.27272727, 0.57142857, 0.5 ]])
データの特徴を捉える値
平均値、中央値、最大値、最小値を計算してみましょう。
まずはサンプルデータを作ります。
今回は標準正規分布 (平均0, 標準偏差1)から値を10個サンプリングしました。
c = np.random.randn(10)
# 結果
array([ 0.74574745, -0.25264616, 2.73971656, 0.01992425, 1.33860227,
0.3727719 , 0.13732889, 0.47620023, 1.32571159, -0.57923272])
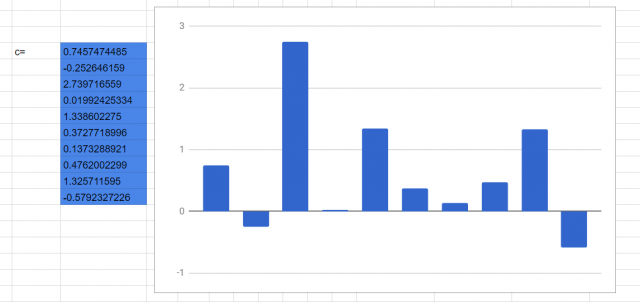
この配列を使って配列を使って計算していきましょう。
平均値
np.mean(c) # 結果 0.6324124270974353
中央値
np.median(c) # 結果 0.4244860647418945
最大値
np.max(c) # 結果 2.7397165593902857
最小値
np.min(c) # 結果 -0.5792327226017869
内積と外積
内積
内積(dot product)、機械学習でよく出てくる計算ですね。
ちょっとわからないぞ?って人は次の記事をチェック。
【数学】「内積」の意味をグラフィカルに理解すると色々見えてくる その1@kenmatsu4 –Qiita
イメージとしては下の感じ。
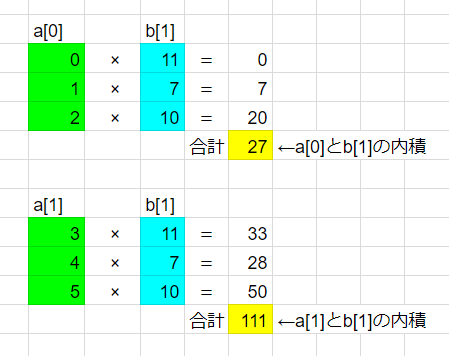
NumPyなら内積の計算も簡単!
result = np.dot(a, c[1]) # 結果 array([ 27, 111])
★ヒント
b[1]
> bの0から数えて1番目の要素を取り出します。つまり[11, 7, 10]が取り出されます。
外積
外積(outer product)・・・というか直積も計算しましょう。
イメージとしては下の感じ。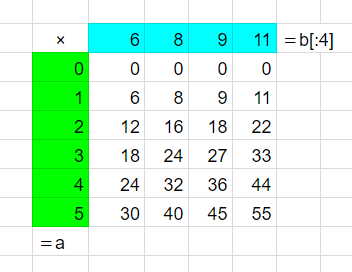 百ます計算(掛け算)みたいな感じですね。
百ます計算(掛け算)みたいな感じですね。
np.outer(a.reshape(6), b.reshape(6)[:4])
# 結果
array([[ 0, 0, 0, 0],
[ 6, 8, 9, 11],
[12, 16, 18, 22],
[18, 24, 27, 33],
[24, 32, 36, 44],
[30, 40, 45, 55]])
まとめ
この記事では、Numpyの簡単な使い方を紹介しました。
NumPyはPythonで非常に重要なライブラリです。
本当に様々なツールで使われていて、これを覚えるだけで世界が広がります。
もっと深いNumPyの勉強がしたい!NumPyで機械学習を実装したい!という方には侍エンジニアのマン・ツー・マンレッスンがオススメです。
[su_button url=”https://lp.sejuku.net/lp1_blog_01/?cid=ai_btn1_59565″ target=”blank” background=”#409fdf” color=”#fff88f” size=”10″ center=”yes” radius=”10″ icon=”icon: external-link” icon_color=”#fff88f” text_shadow=”0px 0px 10px #808080″]侍エンジニアとは?
詳細はこちらから[/su_button]
マン・ツー・マンレッスンでNumPy、機械学習の勉強を始めてみましょう。










