こんにちは!インストラクターのフクロウです。
様々な現象が従うことから、非常に利用頻度の高い確率分布である「正規分布(ガウス分布)」。
この記事ではNumPyで、正規分布に従う乱数を生成する関数であるnp.random.normalを紹介します。
normalという名前がつけられるほど一般的な確率分布です。
いろんな場所で使う関数なので、是非とも覚えておきたいですね。
正規分布とは
正規分布ってなんでしょうか。
例えば、正規分布に従った乱数をたくさん用意しましょう。
これの(bin幅の小さい)ヒストグラムを作ったときに、正規分布に従った乱数は以下のような分布になります。
import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm import matplotlib.pyplot as plt x = np.arange(-10,10,0.01) #ガウス分布の確率密度関数,平均 0、標準偏差1 y = norm.pdf(x,0,1) plt.plot(x,y,color='r') plt.xlim(-10,10)
[Output]
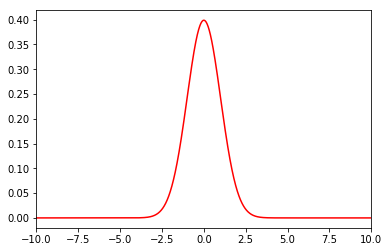
このグラフを確率密度関数と言います。
正規分布の確率密度関数は、このように山のような形になります。
この分布のパラメータは平均と分散(標準偏差)です。
- 平均は山の中心の位置に対応
- 分散(標準偏差)は山の幅に対応
この2つの値を操作することで、上のグラフの形を変えることができるんですね。
自然界の現象を始めとした様々な現象が、この正規分布に従った形になると言われています。
np.random.normalの使い方
標準正規分布に従った乱数の生成
実際に正規分布を使ってみましょう。
np.random.normalを使えば、正規分布に従った乱数を生成することができます。
試しに標準正規分布に従った乱数を生成してみましょう!
(平均0, 分散1の正規分布を標準正規分布と言います。)
基本的な使い方は以下の通り。
a =
np.random.normal(
loc = 0, # 平均
scale = 1, # 標準偏差
size = 1000000,# 出力配列のサイズ(タプルも可)
)
a
[aの要素をoutput]
array([-1.21816181, -0.77891982, 0.78294855, ..., -1.50690286,
2.43792109, -0.43290878])
先程紹介したパラメータの他に、出力配列のサイズを操作する第三引数が加わりました。
平均, 標準偏差, size を指定すれば使えるので、簡単ですね。
これらが本当に正規分布の形になっているのか確認してみましょう。
plt.hist(a,bins=100) plt.xlim(-10,10)
[aのヒストグラム]
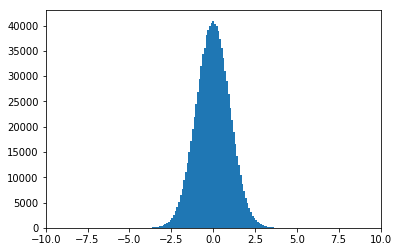
上の確率密度関数のグラフとそっくりのヒストグラムになりましたね!
このようにNumPyを使えば簡単に正規分布を活用することができます。
標準偏差を操作した正規分布
また、パラメータを操作した場合のヒストグラムも見てみましょう。
第二引数のscaleは標準偏差でした。この値を増やしてみます。
b =
np.random.normal(
loc = 0, # 平均
scale = 3, # 標準偏差
size = 1000000,# 出力配列のサイズ(タプルも可)
)
plt.hist(b,bins=100)
plt.xlim(-10,10)
[bのヒストグラム]
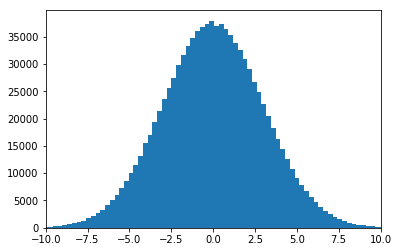
このように太った(幅の広い)山になりました。
標準偏差は、各点の平均点からの距離に対応しています。
この値が大きくなるとヒストグラムは幅が広く、背の低い形になります。
平均を操作した正規分布
次はloc、平均点を操作します。
c =
np.random.normal(
loc = 5, # 平均
scale = 1, # 標準偏差
size = 1000000,# 出力配列のサイズ(タプルも可)
)
plt.hist(c,bins=100)
plt.xlim(-10,10)
[cのヒストグラム]
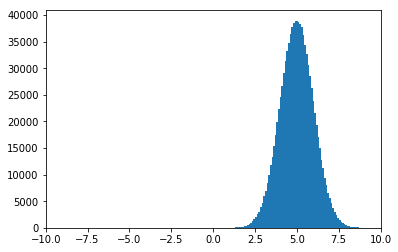
平均の値はヒストグラムの最も度数の大きい階級を操作します。
山の位置を変えたいならばこのパラメータをいじればOKです。
サンプル数を変更
最後に出力される配列の要素数や形状を操作します。
出力値が一次元配列でいいなら100, 200のようなスカラーを渡せばOKです。
二次元以上の配列にしたい場合はタプルでサイズを指定しましょう。
d =
np.random.normal(
loc = 0, # 平均
scale = 1, # 標準偏差
size = 100, # 出力配列のサイズ(タプルも可)
)
plt.hist(d,bins=50)
plt.xlim(-10,10)
[dのヒストグラム]
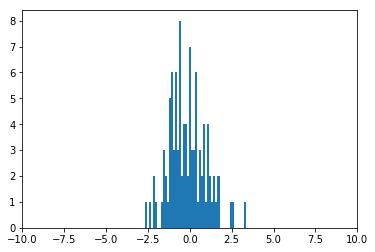
生成した乱数が少ないと、このようにわかりづらい分布になる場合もあります。
サンプル数が多ければ今までのようなヒストグラムになるので、色々と試してみてください。
まとめ
この記事では、np.random.normalを使った正規分布に従った乱数の生成方法を解説しました。
正規分布は機械学習の分野でも様々に利用されています。
例:
- ニューラルネットワークのパラメータの初期化
- ナイーブベイズ分類器の実装
また、この他にもいろんな確率分布があるので、np.randomモジュールを使って試してみてくださいね!









